Pecahan

A. Arti Pecahan

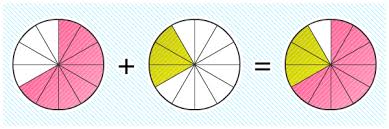
1. Pecahan Sebagai Bagian dari Keseluruhan

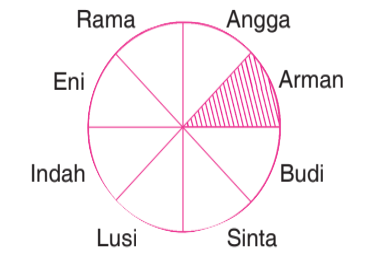
Pernahkah kamu membagi suatu makanan kepada teman-temanmu? Misalnya pada saat kamu ulang tahun. Coba perhatikanlah kue ulang tahun sebelumnya. Kue tersebut dibagi menjadi delapan bagian sama besar. Berapakah bagian Arman dibanding keseluruhan? Bagian Arman adalah 1/8 dari keseluruhan. 1/8 adalah bilangan pecahan dan dibaca “satu per delapan”.

Contoh :

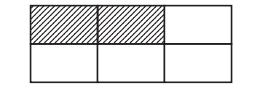Coba kamu lihat gambar di atas, menyatakan pecahan berapakah daerah yang diarsir dibanding keseluruhan?

Jawab :

Yang diarsir = 2 bagian
Keseluruhan = 6 bagian
Jadi, pecahan daerah yang
diarsir adalah 2/6

2. Pecahan yang Berpenyebut Sama

Bagaimana membandingkan dua pecahan yang berpenyebut sama? Untuk membandingkan dua pecahan yang berpenyebut sama, mari memperhatikan gambar di bawah.

Dari gambar diatas 1/4 < 2/4

3. Mengurutkan Pecahan yang Berpenyebut Sama

Untuk mengurutkan pecahan yang berpenyebut sama, caranya sama dengan membandingkan dua pecahan yang berpenyebut sama seperti di atas. Pembilang-pembilang dari pecahan tersebut diurutkan dari yang paling kecil atau urut dari yang paling besar, sesuai dengan yang diinginkan.

Contoh

Mari mengurutkan pecahan-pecahan berikut ini, urut dari yang paling kecil.

5/10 , 2/10 , 7/10 , 9/10 , 4/10 , 6/10

Jawab:

Pembilangnya adalah 5, 2, 7, 9, 4, 6.
Setelah diurutkan dari yang paling kecil, diperoleh: 2, 4, 5, 6, 7, 9.
Jadi, setelah diurutkan dari yang paling kecil, pecahannya menjadi:

2/10 , 4/10 , 5/10 , 6/10 , 7/10 , 9/10

4. Letak Pecahan pada Garis Bilangan

Mari memperhatikan garis bilangan berikut ini.

Garis bilangan di atas menunjukkan bahwa:

1= 3/3

2= 6/3

5. Pecahan Senilai

Berikut adalah contoh video menyelesaikan suatu pecahan

Sumber : https://drive.google.com/file/d/0BxWfzwt3ebPKcmpUTDVDb2VhMGM/view

Latihan Soal

1. Mari menyatakan gambar berikut ke dalam pecahan yang menyatakan bagian yang diarsir terhadap keseluruhan.

2. Mari menyatakan gambar berikut ke dalam pecahan yang menyatakan bagian yang diarsir terhadap keseluruhan.

3. Mari menyatakan gambar berikut ke dalam pecahan yang menyatakan bagian yang diarsir terhadap keseluruhan.

Bilangan Romawi

A. Mengenal Lambang Bilangan Romawi

Lambang bilangan Romawi tidak mengenal bilangan nol. Berikut ini adalah beberapa lambang bilangan Romawi sebagai dasar untuk menuliskan lambang bilangan Romawi yang lain.

Aturan penulisan bilangan Romawi adalah sebagai berikut.
1. Jika angka di sebelah kiri lebih kecil dari angka yang di sebelah kanan, berarti lambang bilangan itu dikurangi.

2. Jika angka di sebelah kanan kurang dari atau sama dengan angka yang di sebelah kiri, berarti dijumlahkan.

Contoh :

a. XX = 10 + 10 = 20
b. VII = 5 + 1 + 1 = 7
c. LV = 50 + 5 = 55

3. Penulisan lambang bilangan Romawi yang sama hanya boleh sebanyak tiga kali berturut-turut.

Contoh :

a. III artinya 1 + 1 + 1 = 3

b. CCC artinya 100 + 100 + 100 = 300

c. XXX artinya 10 + 10 + 10 = 30

Perhatikan bahwa 40 tidak boleh ditulis XXXX (empat kali penulisan lambang yang sama secara berurutan).

4. Aturan pengurangan:

a. I hanya dapat digunakan untuk mengurangi V dan X.
b. X hanya dapat digunakan untuk mengurangi L dan C.
c. C hanya dapat digunakan untuk mengurangi D dan M.

B. Menuliskan Bilangan Asli ke dalam Bilangan Romawi atau Sebaliknya

1. Menuliskan Bilangan Asli ke dalam Bilangan Romawi

Contoh :

Bagaimana bilangan Romawi dari bilangan asli berikut ini?
a. 6 c. 19 e. 245
b. 14 d. 40

Jawab:

a. 6 = 5 + 1
= V I
Jadi, 6 = VI.

b. 14 = 10 + 4
= 10 + (5 – 1)
= X IV
Jadi, 14 = XIV.

c. 19 = 10 + 9
= 10 + (10 – 1)
= X IX
Jadi, 14 = XIX.

d. 40 = 50 – 10
= L – X
= XL
Jadi, 40 = XL.

e. 245 = 200 + 45
= 200 + (50 – 5)
= CC VL
Jadi, 245 = CCVL.

2. Mengubah Lambang Bilangan Romawi ke dalam Bilangan Asli
1. XVI = ….
Jawab:
XVI = 10 + 5 + 1
= 16

2. XIV = ….
Jawab:
XIV = 10 + (5 – 1)
= 10 + 4
= 14

3. LXIII = ….
Jawab:
LXIII = 50 + 10 + 1 + 1 + 1 = 63

4. XXIX = ….
Jawab:
XXIX = 10 +10 + (10 – 1)
= 20 + 9
= 29

Berikut adalahcontoh video bagaimana mengubah bilangan asli kedalam angka romawi

Sumber : https://drive.google.com/file/d/0BxWfzwt3ebPKTTRKZDBJREVsUEE/view

Latihan Soal

1. Bilangan 25 jika ditulis dalam bilangan Romawi adalah ….
2. Bilangan 89 jika ditulis dalam bilangan Romawi adalah ….
3. Bilangan 157 jika ditulis dalam bilangan Romawi adalah ….
4. Bilangan 875 jika ditulis dalam bilangan Romawi adalah ….
5. Bilangan 1945 jika ditulis dalam bilangan Romawi adalah ….

Kelipatan dan Faktor Suatu Bilangan

A. Pengertian Kelipatan dan Faktor

1. Kelipatan suatu Bilangan

Bilangan asli adalah bilangan yang dimulai dari 1, 2, 3, 4,…, dan seterusnya. Jika semua bilangan asli kamu kalikan dengan 2, maka diperoleh bilangan kelipatan dua, yaitu 2, 4, 6, 8, 10, 12, …. dengan cara yang sama, maka:
Bilangan kelipatan 3 adalah 3, 6, 9, 12, 15, 18, ….
Bilangan kelipatan 4 adalah 4, 8, 12, 16, 20, 24, ….

2. Faktor suatu Bilangan

faktor suatu bilangan adalah pembagi habis dari suatu bilangan. Jika bilangan A habis dibagi oleh bilangan B, maka dikatakan B adalah faktor dari A. Bagaimana menentukan faktor suatu bilangan?

Coba perhatikanlah beberapa contoh berikut!

1. Mari menentukan faktor dari 12.
Jawab:
Bilangan 12 diuraikan menjadi perkalian dua bilangan
sebagai berikut.
12 = 1 × 12
= 2 × 6
= 3 × 4
Jadi, faktor dari 12 adalah 1, 2, 3, 4, 6, 12.

2. Mari menentukan faktor dari 16.
Jawab:
Bilangan 16 diuraikan menjadi perkalian dua bilangan
sebagai berikut.
16 = 1 × 16
= 2 × 8
= 4 × 4
Jadi, faktor dari 16 adalah 1, 2, 4, 8, 16.

B. Kelipatan dan Faktor Persekutuan Bilangan

1. Kelipatan Persekutuan Dua Bilangan

Contoh

Bilangan kelipatan 3 adalah 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, ….
Bilangan kelipatan 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …

Ayo tentukanlah kelipatan persekutuan dari 4 dan 5.

Jawab:
Bilangan kelipatan 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ….
Bilangan kelipatan 5 adalah 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …
Jadi, kelipatan persekutuan dari 4 dan 5 adalah 20, 40, 60, ….

2. Faktor Persekutuan Dua Bilangan

Berikut ini adalah contoh faktor persekutuan dari dua bilangan.

1. Faktor dari 8 adalah 1, 2, 4, 8.
Faktor dari 12 adalah 1, 2, 3, 4, 6, 12.
Bilangan-bilangan yang sama dari faktor 8 dan faktor 12 disebut faktor persekutuan dari 8 dan 12.
Jadi, faktor persekutuan dari 8 dan 12 adalah 1, 2, 4.

2. Faktor dari 16 adalah 1, 2, 4, 8, 16.
Faktor dari 18 adalah 1, 2, 3, 6, 9, 18.
Jadi, faktor persekutuan dari 16 dan 18 adalah 1, 2.

3. Bilangan Prima

Bilangan prima adalah bilangan yang tepat memiliki dua faktor. Perhatikanlah faktor dari beberapa bilangan berikut ini!

Faktor dari 2 adalah 1 dan 2.
Jadi, 2 adalah bilangan prima.

Faktor dari 3 adalah 1 dan 3.
Jadi, 3 adalah bilangan prima.

Faktor dari 5 adalah 1 dan 5.
Jadi, 5 adalah bilangan prima.

Bilangan 1 bukan bilangan prima sebab bilangan 1 hanya
memiliki satu faktor, yaitu bilangan 1 itu sendiri. Bilangan 2 adalah satu-satunya bilangan prima yang genap.

Berikut adalah contoh video bagaimana cara menyelesaikan bilangan faktor

sumber : https://drive.google.com/file/d/0BxWfzwt3ebPKaUVsZFhhOTRSZms/view